HISTORIA DEL CÁLCULO

Introducción

El Cálculo constituye una de las grandes conquistas intelectuales de la humanidad. Una vez construido, la historia de la matemática ya no fue igual: la geometría, el álgebra y la aritmética, la trigonometría, se colocaron en una nueva perspectiva teórica. Detrás de cualquier invento, descubrimiento o nueva teoría, existe, indudablemente, la evolución de ideas que hacen posible su nacimiento. Es muy interesante prestar atención en el bagaje de conocimientos que se acumula, desarrolla y evoluciona a través de los años para dar lugar, en algún momento en particular y a través de alguna persona en especial, al nacimiento de una nueva idea, de una nueva teoría, que seguramente se va a convertir en un descubrimiento importante para el estado actual de la ciencia y, por lo tanto merece el reconocimiento. El Cálculo cristaliza conceptos y métodos que la humanidad estuvo tratando de dominar por más de veinte siglos. Una larga lista de personas trabajaron con los métodos "infinitesimales" pero hubo que esperar hasta el siglo XVII para tener la madurez social, científica y matemática que permitiría construir el Cálculo que utilizamos en nuestros días. Sus aplicaciones son difíciles de cuantificar porque toda la matemática moderna, de una u otra forma, ha recibido su influencia; y las diferentes partes del andamiaje matemático interactúan constantemente con las ciencias naturales y la tecnología moderna.

¿qué es el CÁLCULO?

El Cálculo Infinitesimal es la rama de las matemáticas que comprende el estudio y aplicaciones del Cálculo Diferencial e Integral.

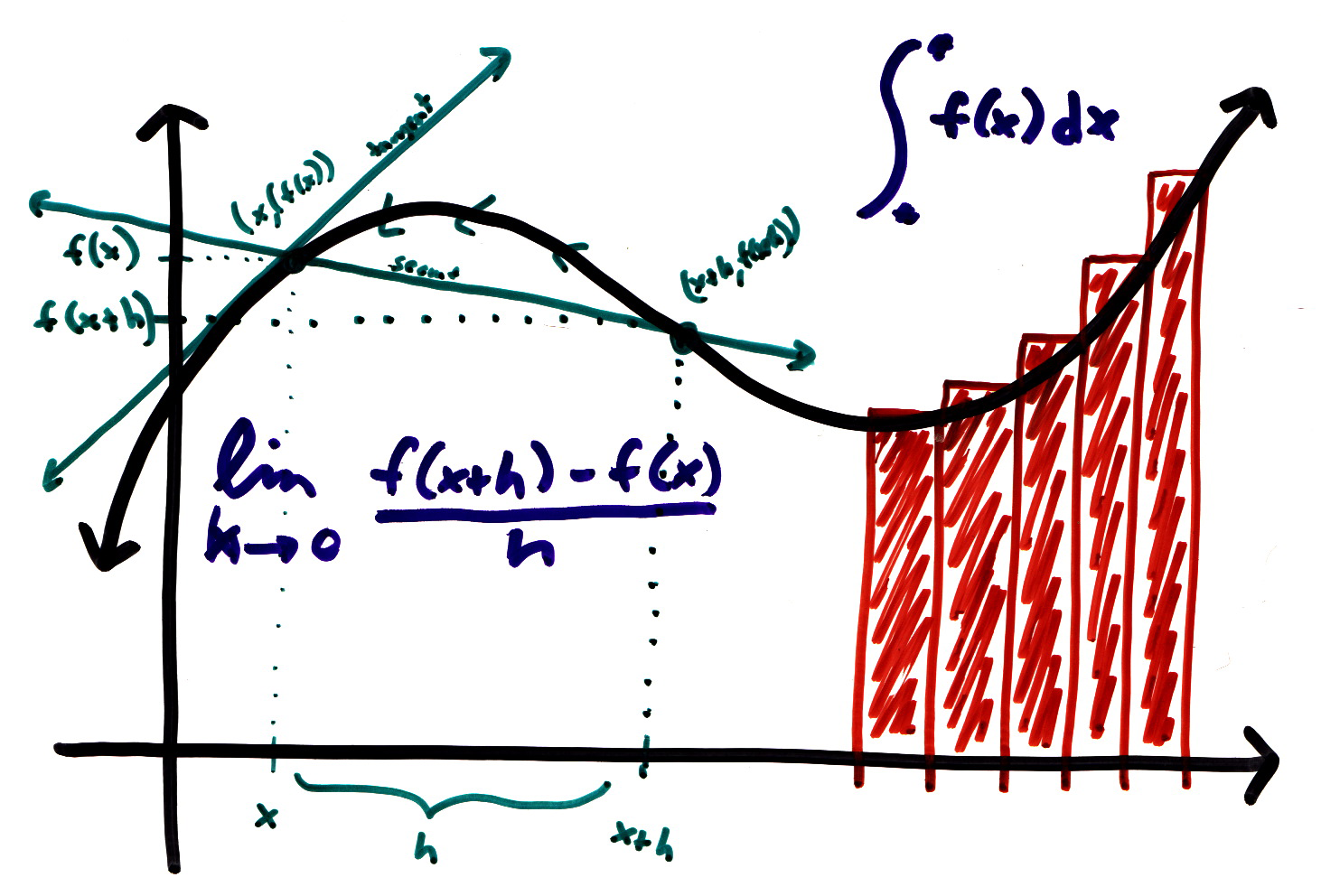
El Cálculo es la matemática del cambio: velocidades y aceleraciones. Cálculo es también la matemática de rectas tangentes, pendientes, áreas, volúmenes, longitudes de arco, centroides, curvaturas y otros diversos conceptos que han hecho que los científicos, ingenieros y economistas puedan modelar situaciones de la vida real.

Aunque las matemáticas previas al cálculo también versan sobre velocidades, aceleraciones, rectas tangentes, etc., aquí se tiene una diferencia fundamental entre las matemáticas previas y el propio cálculo: las matemáticas previas al cálculo son más estáticas, en tanto que el cálculo es más dinámico. El cálculo se interesa en el cambio y en el movimiento; trata de cantidades que se aproximan a otras cantidades.  

antecedentes históricos del cálculo

Los orígenes del cálculo se remontan unos 2500 años por lo menos, hasta los antiguos griegos, quienes hallaron áreas aplicando el “método de agotamiento”. Sabían cómo hallar el área A de cualquier polígono al dividirlo en triángulos (método de triangulación), y sumar las áreas de estos triángulos.  

• MÉTODO DE TRIANGULACIÓN

Establece que cualquier figura plana limitada por líneas poligonales se puede descomponer en triángulos y su área es la suma de las áreas de los triángulos.

• MÉTODO DE AGOTAMIENTO

Es un problema mucho más difícil hallar el área de una figura curva. El método griego de agotamiento consistía en inscribir polígonos en la figura y circunscribir otros polígonos en torno a la misma figura y, a continuación, hacer que el número de lados de los polígonos aumentara. Fue Arquímides (287-212 a.n.e.) quien dio la descripción más clara de este método. 

En 1666 Sir Isaac Newton (1642-1727), fue el primero en desarrollar métodos matemáticos para resolver problemas de esta índole. Inventó su propia versión del cálculo para explicar el movimiento de los planetas alrededor del Sol. Newton concibió el llamado Método de las Fluxiones, considerando a la curva como la trayectoria de un punto que fluye; denomina “momentum” de la cantidad de fluente al arco mucho muy corto, recorrido en un tiempo excesivamente pequeño, llamando la “razón del momentum” al tiempo correspondiente es decir, la velocidad. Por lo tanto, fluente es la cantidad variable que se identifica como función; fluxión es la velocidad o rapidez de variación de la fluente que se identifica como la derivada; al incremento infinitesimal o instantáneo de la fluente se llama momento que se identifica como la diferencial. El principio establece que: “los momentos de las funciones son entre sí como sus derivadas”.

Casi al mismo tiempo, el filósofo y matemático alemán Gottfried Wilhelm Leibniz (1646- 1716), realizó investigaciones similares e ideando símbolos matemáticos que se aplican hasta nuestros días. La concepción de Leibniz se logra al estudiar el problema de las tangentes y su inverso, basándose en el Triángulo Característico de Barrow, observando que dicho triángulo al que se forma con la tangente, la subtangente y la ordenada del punto de tangencia, así mismo, es igual al triángulo formado por la Normal, la Subnormal y la ordenada del mismo punto. La palabra “derivada” y el nombre de “ecuaciones diferenciales” se deben a Leibniz.  

  

EL CÁLCULO EN LA HISTORIA

• El siglo XVII y la disputa por la creación del cálculo

En sus comienzos el cálculo fue desarrollado para estudiar cuatro problemas

científicos y matemáticos:

1. Encontrar la tangente a una curva en un punto.
2. Encontrar el valor máximo o mínimo de una cantidad.
3. Encontrar la longitud de una curva, el área de una región y el volumen de un sólido.
4. Dada una fórmula de la distancia recorrida por un cuerpo en cualquier tiempo conocido, encontrar la velocidad y la aceleración del cuerpo en cualquier instante. Recíprocamente, dada una fórmula en la que se especifique la aceleración o la velocidad en cualquier instante, encontrar la distancia recorrida por el cuerpo en un período de tiempo conocido.

• El siglo XVIII

Durante buena parte del siglo los discípulos de Newton y Leibniz se basaron en sus trabajos para resolver diversos problemas de física, astronomía e ingeniería, lo que les permitió, al mismo tiempo, crear campos nuevos dentro de las matemáticas. Así, los hermanos Bernoulli inventaron el cálculo de variaciones y el matemático francés Monge la geometría descriptiva. Lagrange, también francés, dio un tratamiento completamente analítico de la mecánica, realizó contribuciones al estudio de las ecuaciones diferenciales y la teoría de números, y desarrolló la teoría de grupos. Su contemporáneo Laplace escribió Teoría analítica de las probabilidades (1812) y el clásico Mecánica celeste (1799-1825), que le valió el sobrenombre de "el Newton francés".
Sin embargo el gran matemático del siglo fue el suizo Euler, quien aportó ideas fundamentales sobre el cálculo y otras ramas de las matemáticas y sus aplicaciones. Euler escribió textos sobre cálculo, mecánica y álgebra que se convirtieron en modelos a seguir para otros autores interesados en estas disciplinas. El éxito de Euler y de otros matemáticos para resolver problemas tanto matemáticos como físicos utilizando el cálculo sólo sirvió para acentuar la falta de un desarrollo adecuado y justificado de las ideas básicas del cálculo. La teoría de Newton se basó en la cinemática y las velocidades, la de Leibniz en los infinitésimos, y el tratamiento de Lagrange era completamente algebraico, y basado en el concepto de las series infinitas. Todos estos sistemas eran inadecuados en comparación con el modelo lógico de la geometría griega, y este problema no fue resuelto hasta el siglo posterior.
A los matemáticos de fines del siglo el horizonte matemático les parecía obstruido. Se había llegado al estudio de cuestiones muy complicadas a las que nos se les conocía o veía un alcance claro. Los sabios sentían la necesidad de estudiar conceptos nuevos y hallar nuevos procedimientos.
  

• El siglo XIX

Un problema importante fue definir el significado de la palabra función. Euler, Lagrange y el matemático francés Fourier aportaron soluciones, pero fue el matemático alemán Dirichlet quien propuso su definición en los términos actuales.
En 1821, un matemático francés, Cauchy, consiguió un enfoque lógico y apropiado del cálculo y se dedicó a dar una definición precisa de "función continua". Basó su visión del cálculo sólo en cantidades finitas y el concepto de límite. Esta solución planteó un nuevo problema, el de la definición lógica de número real. Aunque la definición de cálculo de Cauchy estaba basada en este concepto, no fue él sino el matemático alemán Dedekind quien encontró una definición adecuada para los números reales. Los matemáticos alemanes Cantor y Weierstrass también dieron otras definiciones casi al mismo tiempo.
Además de fortalecer los fundamentos del análisis, nombre dado a partir de entonces a las técnicas del cálculo, se llevaron a cabo importantes avances en esta materia. Gauss, uno de los más importantes matemáticos de la historia, dio una explicación adecuada del concepto de número complejo; estos números formaron un nuevo y completo campo del análisis, desarrollado en los trabajos de Cauchy, Weierstrass y el matemático alemán Riemann. Otro importante avance fue el estudio de las sumas infinitas de expresiones con funciones trigonométricas, herramientas muy útiles tanto en las matemáticas puras como en las aplicadas, hecho por Fourier. Cantor estudió los conjuntos infinitos y una aritmética de números infinitos. La teoría de Cantor fue considerada demasiado abstracta y criticada. Encontramos aquí un espíritu crítico en la elaboración de estas nociones tan ricas. Esto constituye un punto de vista muy diferente del que animaba a los matemáticos del siglo anterior. Ya no se trata de construir expresiones ni forjar nuevos métodos de cálculo, sino de analizar conceptos considerados hasta entonces intuitivos.
Gauss desarrolló la geometría no euclidiana pero tuvo miedo de la controversia que pudiera causar su publicación. También en este siglo se pasa del estudio simple de los polinomios al estudio de la estructura de sistemas algebraicos.
Los fundamentos de la matemática fueron completamente transformados durante el siglo XIX, sobre todo por el matemático inglés Boole en su libro Investigación sobre las leyes del pensamiento (1854). 

• Siglo XX y nuestros días

Es importante el aporte realizado por Lebesgue referido a la integración y a la teoría de la medida y las modificaciones y generalizaciones realizadas por matemáticos que lo sucedieron.

En la Conferencia Internacional de Matemáticos que tuvo lugar en París en 1900, el matemático alemán David Hilbert, quien contribuyó de forma sustancial en casi todas las ramas de la matemática retomó veintitrés problemas matemáticos que él creía podrían ser las metas de la investigación matemática del siglo que recién comenzaba. Estos problemas fueron el estímulo de una gran parte de los trabajos matemáticos del siglo.

El avance originado por la invención del ordenador o computadora digital programable dio un gran impulso a ciertas ramas de la matemática, como el análisis numérico y las matemáticas finitas, y generó nuevas áreas de investigación matemática como el estudio de los algoritmos. Se convirtió en una poderosa herramienta en campos tan diversos como la teoría de números, las ecuaciones diferenciales y el álgebra abstracta. Además, el ordenador permitió encontrar la solución a varios problemas matemáticos que no se habían podido

resolver anteriormente.

El conocimiento matemático del mundo moderno está avanzando más rápido que nunca. Teorías que eran completamente distintas se han reunido para formar teorías más completas y abstractas. Aunque la mayoría de los problemas más importantes han sido resueltos, otros siguen sin solución. Al mismo tiempo aparecen nuevos y estimulantes problemas y aún la matemática más abstractas encuentra aplicación.  

fundadores del cálculo

Newton y Leibniz son considerados los inventores del cálculo, o más bien dicho, coinventores, pero representan un eslabón en una larga cadena iniciada muchos siglos antes. Fueron ellos quienes dieron a los procedimientos infinitesimales de sus antecesores inmediatos, Barrow y Fermat, la unidad algorítmica y la precisión necesaria como método novedoso y de generalidad suficiente para su desarrollo posterior. Estos desarrollos estuvieron elaborados a partir de visiones de hombres como Torricelli, Cavalieri, y Galileo; o Kepler, Valerio, y Stevin. Los alcances de las operaciones iniciales con infinitesimales que estos hombres lograron, fueron también resultado directo de las contribuciones de Oresme, Arquímedes y Eudoxo.

Finalmente el trabajo de estos últimos estuvo inspirado por problemas matemáticos y filosóficos sugeridos por Aristóteles, Platón, Tales de Mileto, Zenón y Pitágoras. Para tener la perspectiva científica e histórica apropiada, debe reconocerse que una de las contribuciones previas decisivas fue la Geometría Analítica desarrollada independientemente por Descartes y Fermat.  

contribuyentes al cálulo

• Pierre Fermat (1601-1665): matemático francés, quien en su obra habla de los métodos diseñados para determinar los máximos y mínimos, acercándose casi al descubrimiento del Cálculo Diferencial, mucho antes que Newton y Leibniz. Dicha obra influenció en Leibniz en la invención del Cálculo Diferencial. Fermat dejó casi todos sus teoremas sin demostrar ya que por aquella época era común entre los matemáticos el plantearse problemas unos a otros, por lo que frecuentemente se ocultaba el método propio de solución, con el fin de reservarse el éxito para sí mismo y para su nación, ya que existía gran rivalidad entre franceses, alemanes e ingleses, razón por la que las demostraciones de Fermat se hayan perdido. Hizo además aportaciones a la geometría analítica, la teoría de números y la probabilidad.
• Nicolás Oresme: obispo de la comunidad de Lisieux, Francia, estableció que: en la proximidad del punto de una curva en que la ordenada se considera máxima o mínima, dicha ordenada varía más pausadamente. 
• Johannes Kepler: tiempo después, coincide con lo establecido por Oresme, conceptos que permitieron a Fermat en su estudio de máximos y mínimos, las tangentes y las cuadraturas, igualar a cero la derivada de la función, debido a que la tangente a la curva en los puntos en que la función tiene su máximo o mínimo, es decir, la función es paralela al eje x donde la pendiente de la tangente es nula.
•  Isaac Barrow (Londres, 1630 - id., 4 de mayo,1677): maestro de Newton, construyó el “triángulo característico”, en donde la hipotenusa es un arco infinitesimal de curva y sus catetos son incrementos infinitesimales en que difieren las abscisas y las ordenadas de los extremos del arco.
• Joseph-Louis Lagrange (1736-1813): quien demostró por primera vez el Teorema del Valor Medio. Se dice que Napoleón dijo de él un día: “Lagrange es la altiva pirámide de las ciencias matemáticas”.  
• Leonhard Euler (1707-1783): la simbología f(x) se debe a él, quien además de hacer importantes contribuciones a casi todas las ramas de las matemáticas, fue uno de los primeros en aplicar el cálculo a problemas de la vida real en la Física. Sus extensos escritos publicados incluyen temas como construcción de barcos, acústica, óptica, astronomía, mecánica y magnetismo.  
• John Wallis (Ashford, 23 de noviembre de 1616 – Oxford, 28 de octubre de 1703): enuncia el concepto de “límite”. 
• Simón Lhuilier (n. Ginebra, Suiza el 24 de abril de 1750, f. en Ginebra el 28 de marzo de 1840): la representación simbólica “lím” se debe a él.
• J. G. Leathem: propuso el símbolo “tiende a”.  
• Karl Weierstrass: matemático alemán, se encargó de dar formalidad y estructura a la noción intuitiva de límite.
• Peter Gustav Dirichlet (1805-1859): fue quien dio la primera definición moderna de función. Al principio del desarrollo del cálculo, la definición de función era mucho más restringida que en la actualidad, y no se habían considerado funciones como la de Dirichlet.
• Jacobo Bernoulli: introduce la palabra “función” en el Cálculo Diferencial.
• Niels Henrik Abel (1802.1829) y Evariste Galois (1811-1832): aunque sus vidas fueron breves, sus trabajos en los campos del análisis y del álgebra abstracta fueron de gran alcance.  

otros contribuyentes a lo largo de la historia

ANTES DE CRISTO

THALES DE MILETO (624-547 a.C.)

PITÁGORAS de SAMOS (580-500 a.C.)

ZENÓN DE ELEA (490-425 a.C.)

PLATÓN (427-347 a.C.)

EUDOXO de CNIDUS (408-355 a.C.)

ARQUÍMEDES (287-212 a.C)

SIGLO XVI

LUCA VALERIO (1552-1618)

SIMON STEVIN (1548-1620)

GALILEO GALILEI (1564-1642)

JOHANNES KEPLER (1571 -1630)

RENÉ DESCARTES (1596-1650)

BONAVENTURA CAVALIERI (1598-1647

SIGLO XVII

PIERRE DE FERMAT (1601 -1665)

GILLES DE ROBERVAL (1602-1675)

EVANGELISTA TORRICELLI (1608-1647)

JOHN WALLIS (1616-1703)

BLAIS PASCAL (1623 -1662)

CRISTIAN HUYGENS (1629-1695)

ISAAC BARROW (1630-1677)

ISAAC NEWTON (1643-1727)

GOTTFRIED LEIBNIZ (1646-1716)

MICHEL ROLLE (1652-1719)

JACOB BERNOULLI (1654-1705

JOHANN BERNOULLI (1667-1748)

BROOK TAYLOR (1685-1731)

COLIN MACLAURIN (1698-1746)

SIGLO XVIII

LEONARD EULER (1707-1783)

THOMAS SIMPSON (1710-1761)

ALEXIS CLAUDE CLAIRAUT (1713-1765)

MARIA GAËTANA AGNESI (1718-1799)

JOSEPH LOUIS LAGRANGE (1736-1813)

MARQUÉS DE CONDORCET (1743-1794)

GASPARD MONGE (1746-1818)

PIERRE SIMON DE LAPLACE (1749-1827)

ADRIEN LEGENDRE (1752-1833)

LAZARE CARNOT (1753-1823)

CARL FRIEDRICH GAUSS (1777-1813)

BERNARD BOLZANO (1781 -1848)

AGUSTIN-LOUIS CAUCHY (1789-1857)

GEORGE GREEN (1793-1841)

SIGLO XIX

NIELS ABEL (1802-1829)

KARL WEIERSTRASS (1815-1897)

GEORGE GABRIEL STOKES (1819-1903)

GEORG FRIEDRICH BERNHARD RIEMANN (1826-1866)

RICHARD DEDEKIND (1831 -1916)

JOSIAH WILLARD GIBBS (1839-1903)

GEORG CANTOR (1845-1918)

SOFÍA KOVALEVSKY (1850-1891)

HENRI LÉON LEBESGUE (1875-1941)

SIGLO XX

ANDREY NIKOLAEVICH KOLMOGOROV (1903-1987)

JOHN VON NEUMANN (1903-1957)

JEAN ALEXANDRE EUGENÈ DIEUDONNÉ (1906-1992)

NICOLÁS BOURBAKI (1939-1967)

conclusiones

El progreso de las ideas no se da en el tiempo a través de una trayectoria perfectamente delineada y preconcebida; existen muchos elementos que en la construcción son desechados, reformulados o agregados. Las concepciones filosóficas sobre la realidad, el papel de la ciencia, y en especial las concepciones sobre las características que debe reunir el conocimiento matemático para ser considerado como conocimiento científico, determinaron los enfoques realizados en cada época. El impacto que tuvieron los personajes y las contribuciones consignadas en la historia difícilmente puede ser comprendida cabalmente si estas consideraciones no se toman en cuenta.  

bibliografía

http://www.fca.unl.edu.ar/Intdef/Historia1.htm  

http://recursostic.educacion.es/descartes/web/materiales_didacticos/La_integral_definida_y_la_funcion_area/exhauc.htm

Historia del cálculo.pdf

Un poco de historia y el nacimiento del cálculo.pdf

Cálculo (antecedentes).pdf

https://definicion.de/calculo/